Anita Tjahyadi Blog 4

Definite Integral

Hello class,

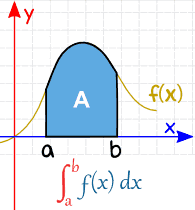
Today I will be helping you learn how to find the area under a curve. The area under a curve, between two points, can be found by doing a definite integral between the two points. 
         

 *Recall: A definite integral is an integral with upper and lower limits. It has start and end values: in other words there is an interval (a to b). With definite integrals, we integrate a function between 2 points, and so we can find the precise value of the integral and there is no need for any unknown constant terms [the constant cancels out].   

To find the area under the curve y = f(x) between x = a and x = b, integrate y = f(x) between the limits of a and b.

                                           Area=∫​a​b​​f(x)dx

__________________________________________________

Example 1: Find the area between y = 7 – x^2 and the x-axis between the values x = –1 and x = 2.

        

Note: If the graph of y = f(x) is partly above and partly below the x-axis, the formula given below generates the net area. That is, the area above the axis minus the area below the axis.

Example 2:  What is the area between the curve y = x^2 -4 and the axis?

*The shaded area is what we want.

*We can easily work out that the curve crosses the x-axis when x= -2 and x= 2. To find the area, therefore, we integrate the fxn b/t -2 & 2.

Areas under the x-axis will come out negative and areas above the x-axis will be positive. This means that you have to be careful when finding an area which is partly above and partly below the x-axis.