B) In my experiment will be a situation in which a Tesla Model S races a quarter mile on a straight track.
C) Time (In Seconds) 0 1 2 3 4 5 6 7 8 9 10
Speed (In Kilometers Per Hour) 0 19 30 50 70 90 102 115 120 128 133
D)
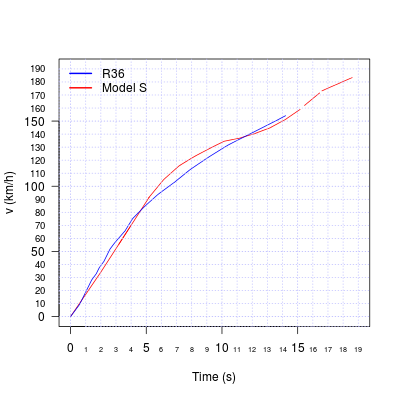
E) points to find secant lines--- (5,90) (6,102) (7,115) (8,120) (9,128)
102-90/6-5=12 km/h
115-90/7-5= 12.5 km/hr
120-90/8-5= 10 km/hr
128-90/9-5= 9.5km/hr
The ARC in these calculations the slopes of the secants grow up until a certain point and then begin to decrease. This means that that over time the car will slowly keep increasing in speed until it reaches its maximum speed.
F)

G) point Q= (1,20)
Slope= 90-20/5-1= 70/4= 17.5km/hr
Mathematically this means that the slope of this line is the rate of change at the very instant at the tangent. This means that at exactly 5 seconds the Tesla is accelerating at 17.5km/hr.
H) I know that this value is in fact the tangent line because the acceleration slows down more and more after 5 seconds and beforehand the it acceleration rate is faster. Since after 5 seconds has a shallow slope and before 5 seconds has a steep slope, I'm confident that the slope I found is the tangent line because it won't touch the graph again.
Jordan, I really like your real life application of a Tesla's speed over a period of time. I don't know anything about sports cars, so it's interesting to see how this Tesla model accelerates at 17.5 km/hr every 5 seconds!
ReplyDeleteCool use of IRC to see a model S's acceleration.
ReplyDeletejordan,
ReplyDeletevery nice application! there is a little bit of an issue with the units that you used. you have your answers expressed as km/hr (which is the only the velocity of the car), but there is the additional unit of seconds. so your units should actually be expressed as velocity per second (which is acceleration), not just km/hr. you explain this later in the post, but when doing your calculations, you should use the correct units. also, i was able to glean it from your calculations, but it would have been great to mention that you were finding the IRC at exactly t = 5 seconds.
your explanations of the meaning of your results are well done! you definitely showed that you understand what it means to calculate the IRC of an object. good job!
professor little