Blog 4 (Power Rule)

Good Evening Class! My name is Professor Ledesma and I am subbing in for Professor Little this class. Today we are learning one of the key concepts in Applied Calculus: Derivatives. Derivatives can be challenging for most students, and I am here to teach you that they are not hard if you follows my easy steps:

This is the definition of the Derivative 

Lets understand how the derivative works:

This above chart explains how the derivative works with my four easy steps:

1. choose an interval 
2. find the raw change 
3. make your model (based on the limit) 
4. find the rate of change 

Its that easy, at the end of the day you are trying to find the slope of the line because lines have infinite number of points on the line.

Lets work out a problem that will be helpful to you:

How dies the function f(x)=x^2 change as we move through the continuum? 

Its that easy! Anyone can be great at calculus! 

Blog 4 (Instantaneous Rate of Change)

Inflection Points

To understand inflection points it is important to be able to distinguish between concave and convex funcitons. A concave function is a function where no line the joins two points on it goes above the graph. A convex function is the opposite (imply below).

It is also important to know what a root is: where the function equals zero.

Before you can find an inflection point you must first find the derivative of the function being graphed.

Find the second derivative (derivative of first derivative) and set it equal to zero.

Your answer will be a possible inflection point.

Find the third derivative of the function to determine whether or not the possible inflection point is truly an inflection point or not. If the answer does not equal zero then it is an inflection point.

To find the coordinates of the inflection point (x, F(x)) calculate the function based on the value of x (which will have been determined earlier in the process).

Plot the coordinates and your inflection point has been found.

Blog 4 (Average Cost)

Jeffrey Williams

Average Cost

So you want to learn about average cost?  Let’s start off with the definition of average cost, average cost is (fixed cost plus variable cost) divided by units produced.  Mathematically, the fixed cost plus variable cost is the cost function which can be represented by the notation C(q) with q being number of units. Since average cost is the cost function divided by the number of units, the formula for average cost is C(q)/q.   We can demonstrate this with a very simple example, suppose that:

Fixed Costs = 10,000

Variable cost per unit = 10

Units produced = 100

So if the cost function is fixed cost + variable cost = cost function (C(q)), then

C(q) = 10,000 + 1,000* = 11,000/10 = 1,100 per unit.

*1,000 is calculated as by taking the variable cost per unit and multiplying it by the units produced to produce total variable cost. Ex: 100 x 10 = 1,000.  

A graph showing average cost compared to the cost function.
 Note how the both graphs eventually meet at 11,000 at 100 units

Okay, so you've learned how to calculated average cost, but why should you need to now this. That's a very good point, the reason why average cost is important is that it allows companies to measure the total cost to produce each unit.  But, isn't variable cost the cost to produce each unit? Well, yes and no; Variable cost is the marginal cost or the cost to produce each unit, but variable costs aren't the only costs that businesses have. Fixed costs are the cost that the business has simply for keeping its doors open. So, even if the business produces zero units it still has a certain amount of costs.  Thus the importance of average cost is it allows businesses to measure the true cost (fixed costs plus variable costs) of each unit it produces. This helps the company determine the profitability of and cost of making more units.  If the marginal or variable cost is less than average cost (MC<AC) then each unit produced become less expensive since the fixed costs of the company are spread out of more units so the cost of each unit decrease.  This decrease in cost increases the business' profits.  The reverse is when marginal cost is greater than average cost (MC<AC) then each unit produced increase cost since each unit cost more produce then the amount it reduces foxed cost per unit.  This increase in cost causes the company to loss money on each unit produced.  To wrap it all up, the cost function and average cost function both measure the same thing (the total cost of a business), the difference between them is how they go about measuring costs.  In the end, you can see in the graph above, they each end at the same amount.

Blog 4

Blog 4 Ashah Alkhater

Hello everyone, I am professor “YYY” and today I am going to explain trapezoidal rule to calculate the area under a curve. Before going to calculate, I will explain the Riemann Sum Review first.

Riemann Sum Review

Let's consider the ramp shown in figure which is characterized by the equation y = x^2 + 1. The area under this curve resembles how much dirt can be remove if someone go from 0 to 2 with a mop. In order to find out how much dirt is going to be removed underneath this ramp, Riemann sum should be used. It considers only one slice along this curve. According to Riemann sum, at first the height somewhere along this curve is measured, and that height is multiplied by 2 meters. That's the distance in x. The height times the width here would the cross-sectional area and tell about how much dirt would be removed.

If a measurement has been made at the far left side, it is a left-side Riemann sum, it gives an area of 2 because the height on the left side is 1 multiplied by the width, which is 2. If a midpoint Riemann sum is considered, area would be estimated at 4. If a right-side Riemann sum is used, the cross-sectional area would be estimated to be 10. This sounds absolutely fantastic, but none of these projections look right.

Area of a trapezoid flipped on its side

So, rather than taking multiple slices and doing a Riemann sum with two different areas, it is not wise to use rectangles and instead estimate this area with a trapezoid.

Using Trapezoids to Estimate Area

The area of a trapezoid is equal to the height of the trapezoid times the average of the two parallel sides.

Area = (Height) * (w sub 1 + w sub 2) / 2

Where, w sub 1 is the length of short edge, and w sub 2 is the long side. Even flipping trapezoid sides still gives the same area, but the height is going along horizontally and w sub 1 on the left side of the trapezoid and w sub 2 on the right side of the trapezoid. Well, this is the function to calculate area.

Therefore, a trapezoid outline is going between the left side, 0, and the right side, 2.

In this case, w sub 1 is the height on the left side, w sub 2 is the height on the right side, and the height is actually the distance between 0 and 2 on the x-axis. If these points are plugged into the area formula, the area equals the value of the function on the left side plus the value of function on the right side all divided by 2 times my delta x. That's the difference between the left-side value of x and the right-side value of x. So in this case, it's 2 - 0.

Using a trapezoid to estimate area on the graph of the function

By plugging in the points for y = x^2 + 1 from 0 to 2. f(x) on the left side is equal to f(0). f(x) on the right side is f(2) - all of that divided by 2 times my delta x, which is 2 - 0. If 0 is plugged into the function y = x^2 + 1, results is 1. If 2 is plugged into that function, result is 5. So the area becomes ((1 + 5) / 2) * 2, and that's just 6.

It can be even better estimated by dividing this into two slices, and take the trapezoid area of two different slices and add them up to get the total sum.

In this way, the first area goes from f(0) to f(1), so the delta x is 1 - 0, and the second area goes from f(1) to f(2), so the delta x is 2 - 1. If the values are plugged in for f(0), f(1) and f(2), the area under the curve is estimated to be 9 / 2.

Similarity, the area can be estimated more accurately if number of the segments becomes higher. Theoretically, the infinite number of segments can give the actual area under the curve.

Blog 4 fahad alhusaini

Anita Tjahyadi Blog 4

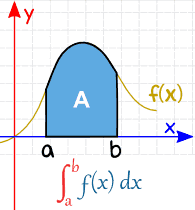Definite Integral

Hello class,

Today I will be helping you learn how to find the area under a curve. The area under a curve, between two points, can be found by doing a definite integral between the two points. 
         

 *Recall: A definite integral is an integral with upper and lower limits. It has start and end values: in other words there is an interval (a to b). With definite integrals, we integrate a function between 2 points, and so we can find the precise value of the integral and there is no need for any unknown constant terms [the constant cancels out].   

To find the area under the curve y = f(x) between x = a and x = b, integrate y = f(x) between the limits of a and b.

                                           Area=∫​a​b​​f(x)dx

__________________________________________________

Example 1: Find the area between y = 7 – x^2 and the x-axis between the values x = –1 and x = 2.

        

Note: If the graph of y = f(x) is partly above and partly below the x-axis, the formula given below generates the net area. That is, the area above the axis minus the area below the axis.

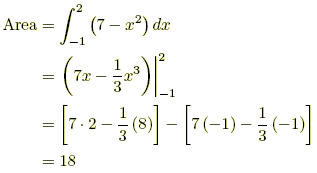
Example 2:  What is the area between the curve y = x^2 -4 and the axis?

*The shaded area is what we want.

*We can easily work out that the curve crosses the x-axis when x= -2 and x= 2. To find the area, therefore, we integrate the fxn b/t -2 & 2.

Areas under the x-axis will come out negative and areas above the x-axis will be positive. This means that you have to be careful when finding an area which is partly above and partly below the x-axis.

Blog 4 Fontaine

My presentation is in the link!

https://docs.google.com/presentation/d/1hVE2eWMvmTuGqo39T19NeDhISiBNGJa6biQF7sH27eU/edit?usp=sharing

CURVE SKETCHING 04/20/2015

CURVE SKETCHING

Hello Class this is our new class that will discuss Curve Sketching. In this class we will be talking about the application of differential calculus.

So, when we sketch a curve we look at several factors.

1- FIRST ORDER DERIVATIVE

X-intercept

We assume y=0 then solve for x.

Y-intercept

We assume x=0 then solve for y.

Find Maxima and Minimum.

Here these points have F’(x)= 0. This means that the first derivative of such a point is equal to zero. The maximum point is represented in the graph below by C while the minimum point is sown by B.

Increasing and decreasing function.

In the graph above, between point A and B the slope of the lines of tangent are negative thus the derivative F’(x) is negative. The function is therefore decreasing between A and B. it is also decreasing between C and D. Between B and C the slope of tangent lines is positive. The graph thus shows an increase between B and C.

Let F be continuous on the interval a<x<b and having derivative f on a<x<b and with a derivative F on a<x<b; then

If F’(x)>0 for a<x<b then F(x) will increase on a< x< b

If F’(x)<0 for a<x<b then F(x) is decreasing

If F’(x)=0 for a<x<b then F(x) is a constant on a<x<b

Up to that point is known as the First Derivative Test.

Example.

Use the First Derivative Test to solve F (x) = x³-27x

Solution.

      X-intercept

X (x²-27) = 0

Intercept at X=0, 5.2 and -5.2

      Y-intercept.

X(x²-27) =y

Y=0

      Maxima and Minima.

F’(x) = 3x²-27

We obtain the critical points when we equate F’(x) to zero.

3(x²-9) =0

(x² -9) =0

(x+3)(x-3)=0

X=-3 or 3

The curve has three sections

(-∞,-3)(-3,3)(3,∞)

This can be represented on the number line as below.

We will look at each interval to determine if it is increasing or decreasing.

In the interval (-∞,-3) we may use x= -5

F’(-5) = 3(-5)² -27 =75 -27 =48 >0

In the interval (-3,3) let x=0

F’(0) = 3(0) -27 = -27< 0

Maximum value F(-3)=(-3)³ – 27 (-3)= -27 + 81= 54

In the interval (3,∞) let x=5

F’(5)=3(5)² – 27= 48 >0

Minimum value F(3)=(3)³ – 27(3) =27 – 81 = -54

Interval	-∞,-3	-3,3	3,∞
F’(x)	positive	negative	positive
curve	Rise	Fall	Rise

2- SECOND ORDER.

We first find the x-intercept as in the first derivative.

From there the y-intercept can be found just like in the first derivative.

Symmetry

This can be found in three different ways

Replacing x by –x in the equation and the equation remains the same. This means it is symmetrical about the y axis.

Replacing y by –y then the sign of the equation changes. This means it is symmetrical about the x-axis.

We may also interchange y with x. this means symmetry about the line y=x

Asymptotes

Vertical asymptotes.

When the denominator of a rational function approaches zero, it has a vertical asymptote. Find the value of x that makes the denominator equal to zero. If your function is y = 1/(x+4), you would solve the equation x+4 = 0, which is x = -4. There may be more than one possible solution for more complex functions. Take the limit of the function as x approaches the value you found from both directions. For this example, as x approaches -4 from the left, y approaches negative infinity; when -4 is approached from the right, y approaches positive infinity. This means the graph of the function splits at the discontinuity, jumping from negative infinity to positive infinity.

Horizontal Asymptotes

The function is y = x/(x-1). Take the limit of the function as x approaches infinity. In this example, the "1" can be ignored because it becomes insignificant as x approaches infinity. Infinity minus 1 is still infinity. So, the function becomes x/x, which equals 1. Therefore, the limit as x approaches infinity of x/(x-1) = 1. Use the solution of the limit to write your asymptote equation. If the solution is a fixed value, there is a horizontal asymptote, but if the solution is infinity, there is no horizontal asymptote. If the solution is another function, there is an asymptote, but it is neither horizontal nor vertical

Maxima and minima

We can then find the maxima and minima of the curve as in the procedure for First Derivative Test.

Point of Inflection.

Let F(x) be differentiable two time [F”(x)] on a< x < b then

If F”(x)>0 for a<x<b then F(x) is Concave upwards.

If F”(x)<0 on a<x<b then F(x) is concave downwards.

If F”(x)=0 or not defined it is a point of inflection.

Example.

Draw the graph y= x⁴ -6x²

Solution

X -intercept y=0

0= x⁴ -6x²

X²(x²-6) = 0

X= 0, 6, -6

Y-intercept x=0

This is at origin.

Maxima and minima

y’ = 4x³ -12x

y’=4x(x+√3)(x-√3)

for maxima and minima put y’=0

then, 4x(x+√3)(x-√3)=0

x=0, √3, √-3

This function has its maxima and minima at (0,0), (-√3, -9) and (√3,9)

 y" = 12x² - 12
Now, y" = 0, then 12(x² - 1) = 0 ⇒ x = -1,1
For point of inflections, if x < -1, y" > 0 and -1 < x < 1, we have y" < 0. So, we get (-1,-5) is one of the point of inflection. Again, if x > 1, y" > 0, at this point again the sign of y" is changed. So, (1, -5) is the point of inflection.