Saturday, April 25, 2015
Thursday, April 23, 2015
Good Evening Class! My name is Professor Ledesma and I am subbing in for Professor Little this class. Today we are learning one of the key concepts in Applied Calculus: Derivatives. Derivatives can be challenging for most students, and I am here to teach you that they are not hard if you follows my easy steps:
This is the definition of the Derivative
Lets understand how the derivative works:
This above chart explains how the derivative works with my four easy steps:
- choose an interval
- find the raw change
- make your model (based on the limit)
- find the rate of change
Lets work out a problem that will be helpful to you:
How dies the function f(x)=x^2 change as we move through the continuum?
Its that easy! Anyone can be great at calculus!
Tuesday, April 21, 2015
Blog 4 (Instantaneous Rate of Change)
Inflection Points
To understand inflection points it is important to be able to distinguish between concave and convex funcitons. A concave function is a function where no line the joins two points on it goes above the graph. A convex function is the opposite (imply below).It is also important to know what a root is: where the function equals zero.
Before you can find an inflection point you must first find the derivative of the function being graphed.
Find the second derivative (derivative of first derivative) and set it equal to zero.
Your answer will be a possible inflection point.
Find the third derivative of the function to determine whether or not the possible inflection point is truly an inflection point or not. If the answer does not equal zero then it is an inflection point.
To find the coordinates of the inflection point (x, F(x)) calculate the function based on the value of x (which will have been determined earlier in the process).
Plot the coordinates and your inflection point has been found.
Blog 4 (Average Cost)
Jeffrey Williams
Average Cost
So you want to learn about average
cost? Let’s start off with the
definition of average cost, average cost is (fixed cost plus variable cost) divided by units
produced. Mathematically, the
fixed cost plus variable cost is the cost function which can be represented by the notation C(q) with q being number of units. Since average cost is the cost function divided by the number of units, the formula for average cost is C(q)/q.
We can demonstrate this
with a very simple example, suppose that:
Fixed Costs = 10,000
Variable cost per unit = 10
Units produced = 100
So if the cost function is fixed cost + variable cost = cost
function (C(q)), then
C(q) = 10,000 + 1,000* = 11,000/10
= 1,100 per unit.
 |
| A graph showing average cost compared to the cost function. Note how the both graphs eventually meet at 11,000 at 100 units |
Okay, so you've learned how to calculated average cost, but why should you need to now this. That's a very good point, the reason why average cost is important is that it allows companies to measure the total cost to produce each unit. But, isn't variable cost the cost to produce each unit? Well, yes and no; Variable cost is the marginal cost or the cost to produce each unit, but variable costs aren't the only costs that businesses have. Fixed costs are the cost that the business has simply for keeping its doors open. So, even if the business produces zero units it still has a certain amount of costs. Thus the importance of average cost is it allows businesses to measure the true cost (fixed costs plus variable costs) of each unit it produces. This helps the company determine the profitability of and cost of making more units. If the marginal or variable cost is less than average cost (MC<AC) then each unit produced become less expensive since the fixed costs of the company are spread out of more units so the cost of each unit decrease. This decrease in cost increases the business' profits. The reverse is when marginal cost is greater than average cost (MC<AC) then each unit produced increase cost since each unit cost more produce then the amount it reduces foxed cost per unit. This increase in cost causes the company to loss money on each unit produced. To wrap it all up, the cost function and average cost function both measure the same thing (the total cost of a business), the difference between them is how they go about measuring costs. In the end, you can see in the graph above, they each end at the same amount.
Monday, April 20, 2015
Blog 4 Ashah Alkhater
Hello everyone, I am professor “YYY”
and today I am going to explain trapezoidal rule to calculate the area under a
curve. Before going to calculate, I will explain the Riemann Sum Review first.
Riemann
Sum Review
Let's consider the ramp shown in figure which is characterized by the equation y = x^2 + 1. The area under this curve resembles how much dirt can be remove if someone go from 0 to 2 with a mop. In order to find out how much dirt is going to be removed underneath this ramp, Riemann sum should be used. It considers only one slice along this curve. According to Riemann sum, at first the height somewhere along this curve is measured, and that height is multiplied by 2 meters. That's the distance in x. The height times the width here would the cross-sectional area and tell about how much dirt would be removed.
If a measurement has been made at
the far left side, it is a left-side Riemann sum, it gives an area of 2 because
the height on the left side is 1 multiplied by the width, which is 2. If a
midpoint Riemann sum is considered, area would be estimated at 4. If a
right-side Riemann sum is used, the cross-sectional area would be estimated to
be 10. This sounds absolutely fantastic, but none of these projections look
right.
Area of a trapezoid flipped on its side
|
So, rather than taking multiple
slices and doing a Riemann sum with two different areas, it is not wise to use
rectangles and instead estimate this area with a trapezoid.
Using Trapezoids
to Estimate Area
The
area of a trapezoid is equal to the height of the trapezoid times the average
of the two parallel sides.
Area = (Height) * (w sub 1 + w sub 2)
/ 2
Where,
w sub 1 is the length of short edge, and w sub 2 is the long
side. Even flipping trapezoid sides still gives the same area, but the height is
going along horizontally and w sub 1 on the left side of the trapezoid
and w sub 2 on the right side of the trapezoid. Well, this is the
function to calculate area.
Therefore, a trapezoid outline is going
between the left side, 0, and the right side, 2.
In this case, w sub 1 is the
height on the left side, w sub 2 is the height on the right side, and the
height is actually the distance between 0 and 2 on the x-axis. If these
points are plugged into the area formula, the area equals the value of the
function on the left side plus the value of function on the right side all
divided by 2 times my delta x. That's the difference between the
left-side value of x and the right-side value of x. So in this
case, it's 2 - 0.
It can be even better estimated by
dividing this into two slices, and take the trapezoid area of two different
slices and add them up to get the total sum.
In this way, the first area goes
from f(0) to f(1), so the delta x is 1 - 0, and the second
area goes from f(1) to f(2), so the delta x is 2 - 1. If the
values are plugged in for f(0), f(1) and f(2), the area
under the curve is estimated to be 9 / 2.
Similarity, the area can be
estimated more accurately if number of the segments becomes higher.
Theoretically, the infinite number of segments can give the actual area under
the curve.
Anita Tjahyadi Blog 4
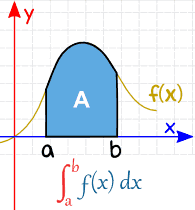 |
| Definite Integral |
Hello class,
Today I will be helping you learn how to find the area under a curve. The area under a curve, between two points, can be found by doing a definite integral between the two points.
*Recall: A definite integral is an integral with upper and lower limits. It has start and end values: in other words there is an interval (a to b). With definite integrals, we integrate a function between 2 points, and so we can find the precise value of the integral and there is no need for any unknown constant terms [the constant cancels out].
Area=∫abf(x)dx
__________________________________________________

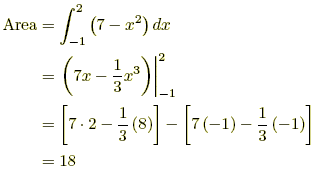
Example 2: What is the area between the curve y = x^2 -4 and the axis?
*The shaded area is what we want.
*We can easily work out that the curve crosses the x-axis when x= -2 and x= 2. To find the area, therefore, we integrate the fxn b/t -2 & 2.
Areas under the x-axis will come out negative and areas above the x-axis will be positive. This means that you have to be careful when finding an area which is partly above and partly below the x-axis.
Blog 4 Fontaine
My presentation is in the link!
https://docs.google.com/presentation/d/1hVE2eWMvmTuGqo39T19NeDhISiBNGJa6biQF7sH27eU/edit?usp=sharing
https://docs.google.com/presentation/d/1hVE2eWMvmTuGqo39T19NeDhISiBNGJa6biQF7sH27eU/edit?usp=sharing
CURVE SKETCHING 04/20/2015
CURVE SKETCHING
Hello Class this is our new class that
will discuss Curve Sketching. In this class we will be talking about the
application of differential calculus.
So, when we sketch a curve we look at
several factors.
1- FIRST ORDER
DERIVATIVE
X-intercept
We assume y=0 then solve for x.
Y-intercept
We assume x=0 then solve for y.
Find
Maxima and Minimum.
Here these points
have F’(x)= 0. This means that the first derivative of such a point is equal to
zero. The maximum point is represented in the graph below by C while the
minimum point is sown by B.
Increasing
and decreasing function.
Let F be continuous on the interval
a<x<b and having derivative f on a<x<b and with a derivative F on
a<x<b; then
If F’(x)>0 for
a<x<b then F(x) will increase on a< x< b
If F’(x)<0 for
a<x<b then F(x) is decreasing
If F’(x)=0 for
a<x<b then F(x) is a constant on a<x<b
Up to that point is known as the First
Derivative Test.
Example.
Use the First Derivative Test to solve F (x) = x3-27x
Solution.
X-intercept
X (x2-27) = 0
Intercept at X=0, 5.2 and -5.2
Y-intercept.
X(x2-27) =y
Y=0
Maxima and Minima.
F’(x) = 3x2-27
We obtain the critical points when we
equate F’(x) to zero.
3(x2-9) =0
(x2 -9) =0
(x+3)(x-3)=0
X=-3 or 3
The curve has three sections
(-∞,-3)(-3,3)(3,∞)
This can be represented on the number line
as below.
We will look at each interval to determine
if it is increasing or decreasing.
In the interval (-∞,-3) we may use x= -5
F’(-5) = 3(-5)2 -27 =75 -27 =48
>0
In the interval (-3,3) let x=0
F’(0) = 3(0) -27 = -27< 0
Maximum value F(-3)=(-3)3 – 27
(-3)= -27 + 81= 54
In the interval (3,∞) let x=5
F’(5)=3(5)2 – 27= 48 >0
Minimum value F(3)=(3)3 – 27(3)
=27 – 81 = -54
Interval
|
-∞,-3
|
-3,3
|
3,∞
|
F’(x)
|
positive
|
negative
|
positive
|
curve
|
Rise
|
Fall
|
Rise
|
2- SECOND
ORDER.
We first find the x-intercept as in the
first derivative.
From there the y-intercept can be found
just like in the first derivative.
Symmetry
This can be found in three different ways
Replacing x by –x
in the equation and the equation remains the same. This means it is symmetrical
about the y axis.
Replacing y by –y
then the sign of the equation changes. This means it is symmetrical about the
x-axis.
We may also
interchange y with x. this means symmetry about the line y=x
Asymptotes
Vertical
asymptotes.
When the denominator of a rational
function approaches zero, it has a vertical asymptote. Find the value of x that
makes the denominator equal to zero. If your function is y = 1/(x+4), you would
solve the equation x+4 = 0, which is x = -4. There may be more than one
possible solution for more complex functions. Take the limit of the function as
x approaches the value you found from both directions. For this example, as x
approaches -4 from the left, y approaches negative infinity; when -4 is
approached from the right, y approaches positive infinity. This means the graph
of the function splits at the discontinuity, jumping from negative infinity to
positive infinity.
Horizontal Asymptotes
The function is y = x/(x-1). Take the
limit of the function as x approaches infinity. In this example, the
"1" can be ignored because it becomes insignificant as x approaches
infinity. Infinity minus 1 is still infinity. So, the function becomes x/x,
which equals 1. Therefore, the limit as x approaches infinity of x/(x-1) = 1.
Use the solution of the limit to write your asymptote equation. If the solution
is a fixed value, there is a horizontal asymptote, but if the solution is
infinity, there is no horizontal asymptote. If the solution is another
function, there is an asymptote, but it is neither horizontal nor vertical
Maxima
and minima
We can then find the maxima and minima of
the curve as in the procedure for First Derivative Test.
Point
of Inflection.
Let F(x) be differentiable two time
[F”(x)] on a< x < b then
If F”(x)>0 for
a<x<b then F(x) is Concave upwards.
If F”(x)<0 on
a<x<b then F(x) is concave downwards.
If F”(x)=0 or not
defined it is a point of inflection.
Example.
Draw the graph y= x4 -6x2
Solution
X -intercept y=0
0= x4 -6x2
X2(x2-6) = 0
X= 0, 6, -6
Y-intercept x=0
This is at origin.
Maxima and minima
y’ = 4x3 -12x
y’=4x(x+√3)(x-√3)
for maxima and minima put y’=0
then, 4x(x+√3)(x-√3)=0
x=0, √3, √-3
This function has its maxima and minima at
(0,0), (-√3, -9) and (√3,9)
y" = 12x2 - 12
Now, y" = 0, then 12(x2 - 1) = 0 ⇒ x = -1,1
For point of inflections, if x < -1, y" > 0 and -1 < x < 1, we have y" < 0. So, we get (-1,-5) is one of the point of inflection. Again, if x > 1, y" > 0, at this point again the sign of y" is changed. So, (1, -5) is the point of inflection.
Now, y" = 0, then 12(x2 - 1) = 0 ⇒ x = -1,1
For point of inflections, if x < -1, y" > 0 and -1 < x < 1, we have y" < 0. So, we get (-1,-5) is one of the point of inflection. Again, if x > 1, y" > 0, at this point again the sign of y" is changed. So, (1, -5) is the point of inflection.
Subscribe to:
Posts (Atom)





















